leetcode-128

128. Longest Consecutive Sequence

Leetcode 128

I solved this problem using C++.
My idea:
use res to store the result、 count to store the current sequence length and max to store the max number of current consecutive.
For loop:
When the sub of two numbers is not greater than 1, we can go to the if statement. If the two numbers are the same, we skip it, or we can add 1 to count and assign the current number to max.
When the sub of two numbers is greater than 1, we can compare res and count, and assign the larger one to res. Then we can reset count to 1 and reset max to the current number.
Finally, we can return the larger one between res and count.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class Solution
{
public:
    int longestConsecutive(vector<int> &nums)
    {
        if (nums.empty())
            return 0;
        int res = 1;
        int count = 1;
        sort(nums.begin(), nums.end());
        int max = nums[0];
        for (int i = 1; i < nums.size(); i++)
        {
            if (abs(nums[i] - max) <= 1)
            {
                // yes
                if (nums[i] == max)
                {
                    // same number
                    continue;
                }
                count += 1;
            }
            else
            {
                // no
                res = res > count ? res : count;
                count = 1;
            }
            max = nums[i];
        }
        return res > count ? res : count;
    }
};

e.g.
input: nums = [9,1,4,7,3,-1,0,5,8,-1,6]
output: 7
explanation:

  1. sort -> [-1,-1,0,1,3,4,5,6,7,8,9]
  2. find the longest consecutive sequence:
    two sequences:
    -1(-1),0,1 -> 3
    3,4,5,6,7,8,9 -> 7
  3. when max is -1, and nums[i] is -1, now abs is not greater than 1, so we can go to the if statement. But they are the same, so we skip it.
    p.s. if we use if (abs(nums[i] - max) <= 1 && nums[i] != max), maybe will go to else statement which is not correct. When they are the same, current consequence is ended and new consequence is started.
  4. when max is 1, and nums[i] is 3, now abs is greater than 1, so we can go to the else statement. We can compare res and count, and assign the larger one to res. Then we can reset count to 1 and reset max to the current number.

However, this solution is not the best one because it uses O(nlogn) time complexity.
We can use O(n) time complexity to solve this problem.

use unordered_set

use unordered_set to store the numbers and remove the duplicates.

for the start of the sequence, we can check if num-1 is not in the set. If it is not, we can start counting the length of the sequence from that number.
Then we can check if num+1 is in the set, and if it is, we can increment the current number and the current result. Finally, we can return the max number of current consecutive.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <vector>
#include <unordered_set>
#include <algorithm>
using namespace std;
class Solution
{
public:
    int longestConsecutive(vector<int> &nums)
    {
        unordered_set<int> num_set;
        for (int num : nums)
        {
            num_set.insert(num);
        }

        int longest_result = 0;
        for (auto num : num_set)
        {
            if (!num_set.count(num - 1)) {
                // not found num-1, so this is the start of a sequence
                int current = num;
                int current_result = 1;
                
                while (num_set.count(current + 1)) {
                    current++;
                    current_result++;
                }

                longest_result = max(longest_result, current_result);
            }
        }
        return longest_result;
    }
};

The time complexity is O(n)!

But in fact, when I use this solution, I find the feedback: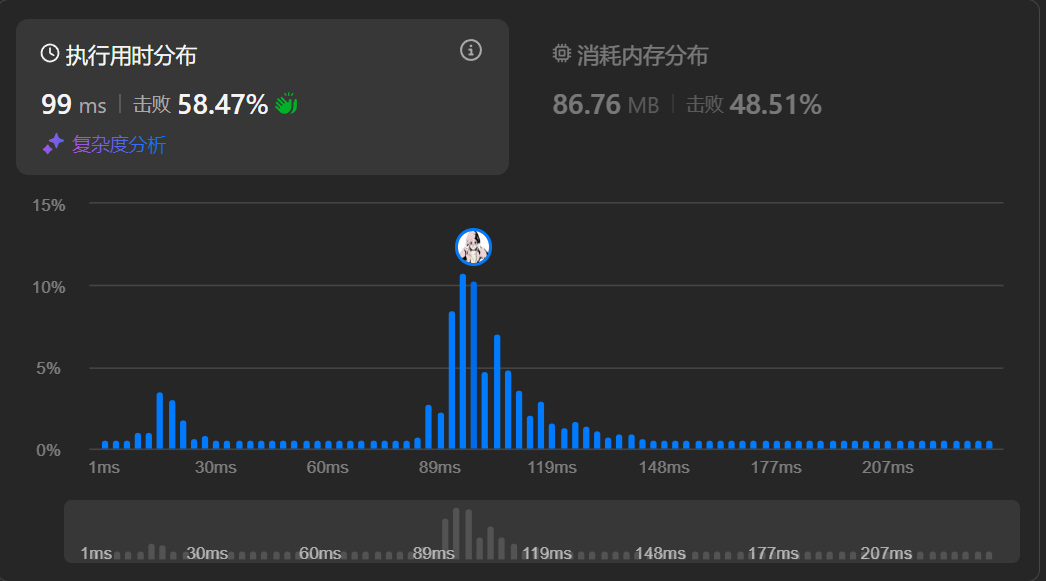
alt text

However the feedback of the first solution is: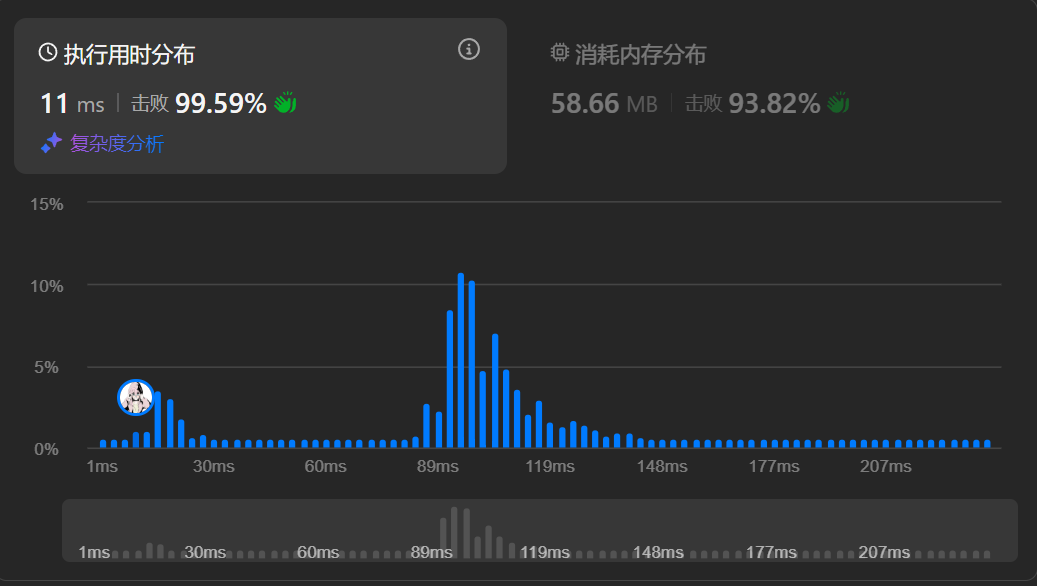
alt text

In fact, unordered_set also takes time…🤣